Netmulticore and the n-queens puzzle

The n-queens puzzle is a well-known toy problem in computer science that can serve as a benchmark for a class of problems where possible solutions are systematically enumerated and then tested whether they fulfill all required properties. Here we show how to speed the algorithm up for multi-core CPU's using the brand-new Netmulticore library for Ocaml.

The exact task is to find all fundamental solutions for a n×n chessboard, then to print the solutions to stdout, and finally to print the number of such solutions. Because of the symmetry of the board we do not count solutions as new when they can be derived from existing solutions by rotation and/or reflection. There are usually eight such equivalent variants, and it does not matter which of the variants representing such a fundamental solution is output by the program.

As we'll see, the restriction to the fundamental solutions makes the algorithm harder to parallelize although the search space becomes smaller. In particular, the algorithm is no longer embarrassingly parallel. The provided solutions would even count as examples of fine-grained parallelism.

Our general design is to first emit all solutions using a brute-force algorithm solve and then to filter out all duplicates that are symmetric to an already found solution. The goal is to look into ways of speeding this design up on multi-core computers, but it is not intended to optimize the core solve algorithm directly. We get then numbers comparing the performance of a parallel algorithm with the basic sequential algorithm, and hopefully an idea how well the parallelization approach worked.

The complete source code is available as example in the newest Ocamlnet test release, which is also available in the Subversion repository: nqueens.ml.

Basic algorithms

The basic data structure is

type board = int array

For such a board array the number board.(col) is the row where the queen is placed in the column col. Rows and columns are numbered from 0 to N-1. For this representation the functions

val x_mirror : board -> board
val rot_90 : board -> board

for reflection at the x (columns) axis and for rotation by 90 degrees are simple array operations (similar to transposition). With their help it is possible to write a function

val transformations : board -> board list

that returns all variants of a solution that can be determined by rotation and reflection (we allow that a variant is returned twice).

Also, we assume we have the core algorithm as

val solve : int -> int -> (board -> unit) -> unit

so that solve q0 N emit generates all solutions where the first queen (in column 0) is put into row q0. For each solution b the function emit b is called to further process it. As already mentioned, this algorithm is expected to find all solutions no matter whether a symmetrical solution is already known or not.

Finally, we assume we can print a board with

val print : board -> unit

SEQ: The sequential algorithm

With the given functions, the sequential solver is simply

  let run n =
    let t0 = Unix.gettimeofday() in
    let ht = Hashtbl.create 91 in
    for k = 0 to n-1 do
      solve k n
        (fun b ->
           if not (Hashtbl.mem ht b) then (
             let b = Array.copy b in
             List.iter
               (fun b' ->
                  Hashtbl.add ht b' ()
               )
               (transformations b);
             print b
           )
        )
    done;
    let t1 = Unix.gettimeofday() in
    printf "Number solutions: %n\n%!" (Hashtbl.length ht / 8);
    printf "Time: %.3f\n%!" (t1-.t0)

We use here a hash table ht to collect all solutions. The hash table is filled with the symmetrical variants, too, so that we can recognize a new fundamental solution by just checking whether it is already member of the table or not.

Runtimes are measured on a single-CPU quad-core Opteron machine (Barcelona) with 8 GB RAM:

Size	Runtime
N=8:	0.001 s
N=9:	0.003 s
N=10:	0.009 s
N=11:	0.039 s
N=12:	0.283 s
N=13:	1.730 s
N=14:	10.037 s
N=15:	66.420 s

The parallel algorithms

There are four parallel versions of this algorithm:

• SHT starts several solvers so that their search spaces do not overlap. The hash table ht is put into shared memory using Netmulticore's Netmcore_hashtbl module. (SHT = shared hash table.)
• SHT2 is an enhanced version trying to address the issue that in SHT several workers struggle for the same lock. In SHT2 we partition the filter space into two distinct sets so that there can be a separate hash table for each set.
• MP does not put the hash table into shared memory but sends all data to a special process that filters duplicates out. This process uses a normal Hashtbl from Ocaml's standard library. (MP = message passing.)
• MP2 is an improved version also partitioning the filter space so that two independent processes perform the filtering.

The performance of the parallel solutions and the sequential original SEQ is depicted in the following diagram. The X axis shows the problem size (N = number of rows/columns of the board), whereas the Y axis is the runtime in seconds (with logarithmic scale).

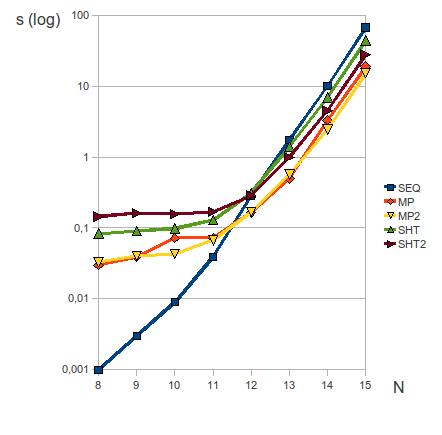
As you can already see, the message passing variants are faster than the versions using a shared hash table. Note that Netmcore_hashtbl is an adaption of Hashtbl using the same hashing technique with even the same hash function. Of course, the shared version has to spend some additional runtime for copying the data to the shared memory block. However, the main problem seems to be that the worker processes lock each other out, because they need exclusive access for adding new elements to the table. The message passing algorithms avoid this problem - Netmulticore's Netmcore_camlbox implementation of message passing allows that several writers send in parallel.

Netmulticore

Ocamlnet has recently been extended by a library for managing multiple processes which can keep/exchange data via shared memory. The library is very new and for sure neither fully optimized nor even bug-free.

The basic design of a Netmulticore program is that several independent Ocaml processes are started so that each process has local memory with its own Ocaml heap, and the usual garbage collector provided by the Ocaml runtime. The processes run at the same speed as in the "uni-core" case, and cannot by random effects step on each others' feet. In addition to this, a pool of shared memory is allocated so that all processes map this memory at the same address. This pool is managed so that additional shared heaps can be kept there. Normal Ocaml data can be moved to a shared heap and accessed like process-local data. Shared heaps must be self-contained so that no pointer references memory outside the same shared heap. Due to these constraints, special coding rules must be followed when shared data is altered. For each shared heap there is a separate garbage collector.

The advantage of this design is there is no "single point of congestion" where several processes would necessarily compete for the same resource (like a single shared heap) and would run into the danger of locking each other out. Although there is a lock for each shared heap granting exclusive write access there is no limit in the number of such heaps. The disadvantage is the self-containment restriction - before data can be accessed by several processes it must be explicitly copied to a shared heap.

SHT: Shared hash tables

The solve function allows it to place the first queen explicitly. We use this feature to split the search space into N partitions: Every parallel worker k puts the first queen into a different row, and the remaining queens are systematically tried out.

There is a trick to reduce the number of write accesses to the hash table by a factor of eight. Instead of adding all solutions to the table only a representative of each fundamental solution is entered. The representative is simply the smallest board according to Ocaml's generic comparison function.

This leads to this worker implementation:

  let worker (pool, ht_descr, first_queen, n) =
    let ht = Netmcore_hashtbl.hashtbl_of_descr pool ht_descr in
    solve first_queen n
      (fun b ->
	 let b = Array.copy b in
	 let b_list = transformations b in
	 let b_min =
	   List.fold_left
	     (fun acc b1 -> min acc b1)
	     (List.hd b_list)
	     (List.tl b_list) in
	 let header = Netmcore_hashtbl.header ht in
	 Netmcore_mutex.lock header.lock;
	 try
	   if not (Netmcore_hashtbl.mem ht b_min) then (
	     Netmcore_hashtbl.add ht b_min ();
	     print b_min
	   );
	   Netmcore_mutex.unlock header.lock;
	 with
	   | error ->
	       Netmcore_mutex.unlock header.lock;
	       raise error
      )

Note that we have to use a lock to make the whole read/write access atomic (the Netmcore_hashtbl module already uses locks to protect each access operation individually, but this is not sufficient here). The call of Netmcore_hashtbl.add differs from Hashtbl.add in so far the keys and values to add are first copied to the shared heap.

The full implementation also has a controller process which starts the workers and waits until all workers are finished. Finally, the number of solutions is the length of the shared hash table.

The problem of this solution is that only one of the worker processes can have the lock at a time. The runtime required for adding an element to the shared hash table is substantially higher than in the sequential case because of the additional copy done by Netmcore_hashtbl.add, making the locking issue even more problematic. However, in the end SHT is faster than SEQ for N >= 13. (For smaller N the time for setting up the processes and the shared memory pool - needing a few RPC calls in the current Netmulticore implementation - lets the sequential version win.)

Size	Runtime
N=8:	0.083 s
N=9:	0.090 s
N=10:	0.098 s
N=11:	0.129 s
N=12:	0.312 s
N=13:	1.387 s
N=14:	6.890 s
N=15:	43.739 s

SHT2: Two shared hash tables

As we have a representative for each fundamental solution, it is easily possible to provide more than one hash table, and to use each table for a subset of the solutions. Here, we check this idea with two hash tables.

The worker now looks as follows:

  let worker (pool, ht1_descr, ht2_descr, first_queen, n) =
    let ht1 = Netmcore_hashtbl.hashtbl_of_descr pool ht1_descr in
    let ht2 = Netmcore_hashtbl.hashtbl_of_descr pool ht2_descr in
    solve first_queen n
      (fun b ->
	 (* Because this is a read-modify-update operation we have to lock
	    the hash table
	  *)
	 let b = Array.copy b in
	 let b_list = transformations b in
	 let b_min =
	   List.fold_left
	     (fun acc b1 -> min acc b1)
	     (List.hd b_list)
	     (List.tl b_list) in
	 let ht = if b_min.(0) < n/2 then ht1 else ht2 in
	 let header = Netmcore_hashtbl.header ht in
	 Netmcore_mutex.lock header.lock;
	 try
	   if not (Netmcore_hashtbl.mem ht b_min) then (
	     Netmcore_hashtbl.add ht b_min ()
	   );
	   Netmcore_mutex.unlock header.lock;
	 with
	   | error ->
	       Netmcore_mutex.unlock header.lock;
	       raise error
      )

Note that we exploit here the fact that each hash table lives in a shared heap of its own. Because of this, there is no hidden common lock where the two table implementations could run into a congestion issue.

The results show that this idea works. The SHT2 version is quite a bit faster although not twice as fast:

Size	Runtime
N=8:	0.145 s
N=9:	0.162 s
N=10:	0.157 s
N=11:	0.169 s
N=12:	0.286 s
N=13:	0.999 s
N=14:	4.503 s
N=15:	28.027 s

I've not examined whether the idea can be generalized to more than two hash tables. This is probably the case.

MP: Workers passing messages to a filter process

The shared hash tables have the disadvantage that the accesses to them are practically serialized. Even worse, the CPU cores have to wait on each other, requiring an expensive form of synchronization. By changing the design, we try to address this problem differently.

In this version of the algorithm the worker processes do not filter out the duplicates, but just send all result candidates to a special collector process. The collector uses then a normal process-local hash table to do the filtering.

This program uses Netmcore_camlbox and Netcamlbox for message passing. The (single) receiver of the messages has to create the box, and the (multiple) senders can put messages into the slots of the box. Because there are several slots for messages, the senders can normally avoid to compete for the same locks.

Of course, the workers put only the representatives of the fundamental solution into the box, leading to this piece of program:

  let worker (camlbox_id, first_queen, n) =
    let cbox = 
      (Netmcore_camlbox.lookup_camlbox_sender camlbox_id : camlbox_sender) in
    let current = ref [] in
    let count = ref 0 in

    let send() =
      Netcamlbox.camlbox_send cbox (ref (Boards !current));
      current := [];
      count := 0 in
    
    solve first_queen n
      (fun b ->
	 let b = Array.copy b in
	 let b_list = transformations b in
	 let b_min =
	   List.fold_left
	     (fun acc b1 -> min acc b1)
	     (List.hd b_list)
	     (List.tl b_list) in
	 current := b_min :: !current;
	 incr count;
	 if !count = n_max then send()
      );
    if !count > 0 then send();
    Netcamlbox.camlbox_send cbox (ref End)

There is the further optimization that we consider a list of boards as a message, and not a single board, reducing the overhead for message passing even more. The last message is End, signalling to the collector that all solutions have been sent.

The collector looks now as follows (some parts omitted for brevity):

  let collector n =
    let msg_max_size =
      ((n+1) * 3 * n_max + 500) * Sys.word_size / 8 in

    let ((cbox : camlbox), camlbox_id) =
      Netmcore_camlbox.create_camlbox "nqueens" (4*n) msg_max_size in

    ... (* start workers *)

    let ht = Hashtbl.create 91 in
    let w = ref n in
    while !w > 0 do
      let slots = Netcamlbox.camlbox_wait cbox in
      List.iter
	(fun slot ->
	   ( match !(Netcamlbox.camlbox_get cbox slot) with
	       | Boards b_list ->
		   List.iter
		     (fun b ->
			if not (Hashtbl.mem ht b) then (
			  let b = Array.copy b in
			  Hashtbl.add ht b ();
			  print b
			)
		     )
		     b_list
	       | End ->
		   decr w
	   );
	   Netcamlbox.camlbox_delete cbox slot
	)
	slots
    done;

    ... (* wait for termination of workers *)

    printf "Number solutions: %n\n%!" (Hashtbl.length ht)

The MP version of the program still has a bottleneck, namely the single collector process. Nevertheless, it already performs better than the versions using shared hash tables:

Size	Runtime
N=8:	0.030 s
N=9:	0.039 s
N=10:	0.072 s
N=11:	0.072 s
N=12:	0.166 s
N=13:	0.501 s
N=14:	3.298 s
N=15:	18.806 s

MP2: Two filter processes

Of course, the same idea as in SHT2 can also be applied here. This leads to MP2: Two filter processes are started, and each process is in charge for filtering one half of the search space.

There is a difficulty, though: For getting the exact count of the results we have to merge the result sets of both collector processes. We do this here (in a bit inefficient way) by sending all results to a master collector where they can be counted. This design leads to the next difficulty: The message boxes for the two collectors cannot be created before starting the workers. Because of this, the workers have to wait until the message boxes are created. We use condition variables for doing so.

Although the algorithm gets complicated by this design, there is nothing really new, and we omit it here in the article. The results are impressive, we can even observe a super linear speedup for N >= 14:

Size	Runtime
N=8:	0.033 s
N=9:	0.040 s
N=10:	0.043 s
N=11:	0.067 s
N=12:	0.169 s
N=13:	0.568 s
N=14:	2.455 s
N=15:	15.215 s

The highly interesting point is that the design of the message passing algorithm wins although the data is even sent twice between processes (and copied twice). It is not the runtime of the individual operation that counts but whether the parallely executed operations lock each other out or not. The message passing algorithm avoids lock situations between CPU cores. Also, it is a bit more coarse-grained because several solutions can be bundled into a single message.

Note that this does not mean that message passing is always better. This is just an example where it leads to a smoother way of execution, mainly because we can organize the data stream without feedback loops.

Of course, this article is also meant to demonstrate that programming with Netmulticore is not that complicated and relatively high-level. The programmer needs not to deal with representations of data, for instance (i.e. no need for a data marshalling format). Also, the shared data structures like Netmcore_hashtbl work well enough so that we see a speedup even for a fine-grained parallelization design like SHT. This may also work for other problems, especially scientific ones, where (easier) coarse-grained designs are often not possible.