Parallelizing with Ocamlnet

O'Caml seems not be recognized as a programming language where it is easy to parallelize tasks. Recently, there was a heated discussion on caml-list about this subject, and people complained that the memory management of O'Caml does not work well for multi-threaded programs. Actually, the memory manager enforces that only one O'Caml thread can execute code at any time, so that there is no way to make efficient use of multi-core CPUs. Well, there are ways around this limitation, and in this article I'll show how to multiply matrices in a distributed system. We don't use multi-threading, but multi-processing which means that the threads of execution don't have easy access to shared memory. For communication and synchronization we use remote procedure calls which can basically do the same as shared memory, but at higher cost. Most important, however, is that the restriction of the O'Caml memory manager no longer applies: The processes are independent, and every process has its own manager.

In order to tackle problem we need a way to break down the algorithm so that the running processes don't have to synchronize with each other often. This is very easy for the matrix multiplication (but may be more complicated for other problems): Every cell of the result matrix is the scalar product of one column of the first input matrix with one row of the second input matrix. Thus the cells can be computed independently, and one only has to take care that all processes have access to the input matrices, and that the processes do not interfer with each other when writing the results.

The tools

In this solution of the problem we use the toolset provided by Ocamlnet. It includes a mature and quite efficient implementation of SunRPC we'll use for interprocess communication. Furthermore, there is Netplex for creating and managing multi-process servers. The plan is to create an RPC service for multiplying matrices that can take advantage of several cores and that can even run in a compute cluster.

The Netplex/SunRPC combination is quite powerful. Basically, a SunRPC server accepts TCP connections, and executes the incoming RPC calls. With our tools we can choose whether we want to have a single process that processes all connections, or whether we want to create new processes for every connection. Obviously, the latter is the way to go for doing the hard computation work, because O'Caml allows us only to take advantage of several cores by running the code in different processes. The single process choice is also useful, namely for controlling the computation, i.e. for synchronization. In this example we'll use both types of process management.

SunRPC is a quite aged standard for doing remote procedure calls. RPC is typed message passing, that means we cannot only pass strings from one process to the other, but values of all types of the interface definition language. In SunRPC we have ints, floats, strings, arrays, options, records ("structs"), and variants ("unions"). Furthermore, RPCs are usually "two-way" messages: Input messages are always replied with output messages.

The components

We have two components. One is called the "controller" and manages the work to do. Actually, the controller defines the outer loops of the algorithm. Furthermore, there is the "worker" component. The worker can be instantiated several times (and runs then in several processes). It implements the inner loop of the algorithm that runs in parallel.

The general idea is that the controller triggers the workers when a new multiplication is to be done, and that the workers are themselves repsonsible for getting the input data, and for getting the tasks to execute. In the SunRPC IDL this looks like:

program Controller {
    version V1 {
	void ping(void) = 0;

	dim get_dim(which) = 1;
	/* Workers can call this proc to get the dimension of the matrix */

	row get_row(which,int) = 2;
	/* Workers can call this proc to get a row of the matrix. The int
           is the row number, 0..rows-1
	*/

	jobs pull_jobs(int) = 3;
	/* The controller maintains a queue of jobs. This proc pulls a list
           of jobs from this queue. The int is the requested number.
	*/

	void put_results(results) = 4;
	/* Put results into the result matrix. */
	
    } = 1;
} = 2;


program Worker {
    version V1 {
	void ping(void) = 0;

	void run(void) = 1;
	/* The controller calls this proc to initiate the action in the worker.
           When it returns, it is assumed that the worker is completely
           finished with everything.
	*/
    } = 1;
} = 3;

(There is also a program Multiplier with program number 1 we'll show later.)

These are the procedures the two components expose. When a multplication is to be done, the order of actions is as follows:

1. We assume the controller has the input data. The controller calls the "run" RPC of all workers to trigger them.
2. The workers now fetch the input data from the controller by calling "get_dim" and then "get_row" until they have all input values.
3. The workers now run jobs from the controller by repeatedly calling "pull_jobs", then executing the jobs, and finally transmitting the results back to the controller by invoking "put_results". The workers can pull several jobs at one, and they can put several results at once. This reduces the relative costs of the RPC overhead per job.
4. The workers are done when there are no more jobs, i.e. the list of jobs pulled from the controller is empty. Now they can pass back the result message of "run" to the controller.

Note that the controller must be able to do several things in an overlapped way: After it has sent the input messages to the "run" RPC of the workers it must be responsive and accept incoming RPC calls from the workers. Finally it must wait until all result messages from the "run" RPCs have arrived. Ocamlnet's RPC implementation supports such overlapped RPC execution. (Note that Sun's original implementation does not support this!)

The Multiplier program is just another interface of the controller. It is the public interface used by the client of the multiplier:

program Multiplier {
    version V1 {
	void ping(void) = 0;
	
	void test_multiply(int,int,int) = 1;
	/* Creates a test matrix with random values and multiplies them.
	   Args are: (l_rows, r_cols, l_cols = r_rows)
	*/
    } = 1;
} = 1;

The implementation

The complete source code is available here:

• code/examples/rpc/matrixmult

It will also be available in future releases of Ocamlnet, but for now it is only accessible via Subversion.

Of course, using a distributed approach creates a lot of coding overhead. Compare with the direct implementation in simple.ml (also in this directory): The multiplication algorithm counts there only 9 lines of code. Compared with that we had to develop a lot of additional stuff: 389 lines for the distributed implementation. This is the price we have to pay in terms of coding effort.

Netplex requires a configuration file, here mm_server.cfg. Basically, the file lists the components that are supposed to accept incoming connections. Here, it looks like:

netplex {
  ...
  service {
    name = "mm_controller";
    protocol { ... };
    processor {
      type = "mm_controller";
      worker { host = "localhost"; port = 2022 };
      worker { host = "localhost"; port = 2022 };
    };
    workload_manager { ... };
  };

  service {
    name = "mm_worker";
    protocol { ... };
    processor {
      type = "mm_worker";
      controller_host = "localhost";
      controller_port = 2021;
    };
    workload_manager { ... };
  };
}

We have omitted boring parts ("..."). We configure the mm_controller that connects with two workers, both reachable over TCP port localhost:2022, and the mm_workers talking to the controller over port localhost:2021. By including the same worker port twice in the list of workers, two independent connections are created, and because of the worker configuration two processes are started. (This is configured in the omitted workload_manager block.)

Netplex starts exactly the components it finds in the configuration file, even if more components are implemented in the code. This is quite useful, because the same binary can be used for different setups. In this example, we could run the multiplication server on host X with both controller and workers, and on host Y with only the workers.

Some numbers

I've done some performance tests on a Opteron 2212 system with 2 CPUs and each CPU has 2 cores (i.e. 4 cores in total). The tests were done in 64 bit mode and ocamlopt-compiled programs. The interesting question is not the total performance, but how much overhead we have by the message passing, and how scalable the system is.

The test is to square an NxN matrix of random numbers, for N=1000, N=2000, and N=3000. This has been done with the non-distributed version of the multiplation (simple.ml), and with the distributed version and W workers, for W=1, W=2, and W=4.

What we expect is that for larger input matrices the relative cost of message passing drops, because we have to transfer the input matrix only once for every worker, and the result matrix only once in total, but the computation time for the multiplication is O(N³) compared to O(N²) for message passing.

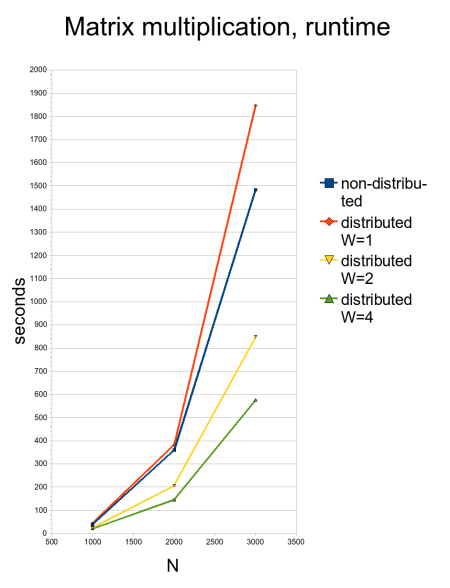
Here are the runtimes, as table, and as diagram:

Test	N	Runtime (seconds)
Non-distributed	1000	38.61
Non-distributed	2000	359.765
Non-distributed	3000	1483.759
Distributed, W=1	1000	45.174
Distributed, W=1	2000	382.874
Distributed, W=1	3000	1847.225
Distributed, W=2	1000	24.407
Distributed, W=2	2000	206.426
Distributed, W=2	3000	849.089
Distributed, W=4	1000	20.842
Distributed, W=4	2000	144.718
Distributed, W=4	3000	576.02

Not bad, right? The time spent for message passing seems to be acceptable. If you compare the non-distributed time for N=3000 with the time of the distributed system and one worker, the overhead is approximately 25% of the total runtime.

For larger W the overhead for the initial transfer of the input matrices increases - they have to be copied to every worker. The algorithm can be improved here, because the controller process becomes soon the bottleneck as it has to copy the matrices for every worker. Alternatively, the matrices could be spread among the workers by the workers themselves in order to get a better degree of parallelization during the transfer phase.

As last, fun test I started workers on three nodes so that in total 10 cores were available (I couldn't do more because I did not find more idle systems in Wink's cluster). I got a runtime of 349 seconds for N=3000. As the cores were not identical, this does not tell us much except that we really can do it over the network, and that this multiplier really takes advantage of a cluster.